Variational AutoEncoder를 이해하기 위해서는 기존의 머신러닝 관점을 확률론적 관점으로 바라볼 수 있어야 합니다. 해당 글은 이활석님의 오토인코더의 모든것이라는 강연을 보고 정리한 느낌이 되겠습니다. 이번 포스팅에서는 아래의 문구를 이해하는데 초점을 맞추며 내용을 이어갈 계획입니다.
딥러닝 모델을 학습시킨 다는 것은 Maximum Likelihood Estimation 하는 것과 같은 말이다.
기존의 머신러닝 학습 과정
우리가 일반적으로 머신러닝을 처음 공부할 때, 아래와 같은 메커니즘으로 모델이 동작한다는것을 배웁니다.

- 학습데이터 x를 모델에 입력한다.
- 입력값 x가 모델 내의 파라미터(Weight and Bias)를 거쳐가며 예측값인 y_pred를 출력해 낸다.
- 이렇게 얻은 예측값 y_pred 와 실제값인 y_true 사이의 오차를 구한다. 이때 오차를 구하는 방식으로 크게 MSE와 Cross-Entropy가 있다.
- 해당 오차인 Loss값이 줄이는 방향으로 모델을 학습시킵니다. 보통 Gradient Descent방법론으로 모델의 파라미터를 새롭게 갱신한다.
- 위의 과정을 계속 반복하며, 오차가 충분히 줄어들 때까지 학습을 진행한다.
위의 내용은 머신러닝의 핵심이자, 가장 먼저 배우는 내용이 될 것입니다. 그래서 “기존의 머신러닝”이라고 소제를 짓게 되었습니다. 하지만 아래의 “확률 관점으로 보는 머신러닝”에서는 위와는 사뭇 다른 해석을 하게 됩니다. 해당 관점으로 넘어가기 전 우리는 기존의 머신러닝에 대해 2가지만 기억하고 지나가 봅시다.
1. 출력값 : 고정 입력(x)에 대한 고정 출력(y_pred)을 얻게 된다.
2. Loss : 출력값과 실제값이 얼마나 차이나는지에 의해 오차(Loss)가 결정된다. MSE or CrossEntropy
Likelihood와 MLE(Maximum Likelihood Estimation)
후에 확률 관점으로 머신러닝을 바라보기 위해서는 Likelihood와 MLE의 개념에 대해 숙지할 필요가 있습니다. 뿐만 아니라, 여러 생성모델들을 설명하는 데에 있어서도 자주 언급되는 용어다 보니 이번기회에 직관적인 이해를 하고 넘어가면 좋을 것 같습니다.
1) Likelihood
Likelihood를 한 문장으로 요약하자면 “데이터가 특정 확률 분포로부터 나왔을 확률”이라 설명할 수 있습니다. 좀더 풀어서 예시를 통해 이해해 보겠습니다. 아래와 같이 남자의 키 10개가 담긴 데이터가 있다고 가정하며, 이를 표현하고자 하는 여러 확률 분포를 그려 보면 아래와 같습니다. 이때 남자의 키는 정규분포를 따른다고 가정하겠습니다.(이 가정이 매우 중요합니다. 이러한 가정 없이는 데이터를 잘 근사화할 확률 분포를 정의하기가 힘듭니다.)

위의 3개의 분포 중에서 남자의 키 데이터를 가장 잘 표현하고 있는 분포는 어떤걸까요? 아마 직관적으로 A분포가 가장 잘 표현하고 있다고 느끼실 겁니다. 잘 나타냄의 정도를 수치적으로 나타내기 위해 우리는 Likelihood를 구할 수 있겠습니다. 위의 10개의 남자 키 데이터를 각각의 확률 분포(A, B, C)에 넣어 얻은 확률들을 모두 곱한 값(Likelihood)을 비교해 보면 됩니다. 그렇게 하면 A에 해당하는 Likelihood 값이 가장 큰 값이 나올 것입니다. 이를 수식으로 표현해 보면 아래와 같습니다.

위의 수식에서 $\theta$는 확률 분포를 결정짓는 파라미터라 볼 수 있겠는데요, 위의 예시에서는 확률 분포를 정규분포로 가정했기에, $\theta$는 평균과 표준편차가 될 수 있겠네요. 따라서 남자의 키 데이터에선 A 분포의 $\theta$를 가질 때, Likelihood값이 가장 높다는걸 알 수 있습니다. 이처럼 Likelihood는 해당 확률 분포(A, B, C)가 특정 데이터(남자의 키 데이터)를 얼마나 잘 표현하고 있는지 나타내는 수치로 사용될 수 있습니다.
2) MLE(Maximum Likelihood Estimation)
MLE(Maximum Likelihood)는 특별한것 없이, 위에서 구한 Likelihood값이 최대가 되도록 하는 것입니다. 즉, 주어진 데이터를 가장 잘 표현하는 확률 분포를 구해 내는 과정이라 해석할 수 있죠. 위의 예시를 다시 한번 보겠습니다. 초기에 우리가 구한 분포가 만약 C분포라면, 이를 A분포와 같이 데이터를 잘 표현하는 분포로 변형될 필요가 있습니다. 이를 위해 Likelihood가 높아지는 방향으로 $\theta$를 변형해 줄 수 있으며, C → B → A 방향으로 분포가 점점 이동할 것입니다. 이러한 과정을 MLE라 하며, 수식으로 표현하면 아래와 같습니다.

그리고 해당 수식을 다르게 표현해 보면 아래와 같이 표현해 볼수도 있죠.
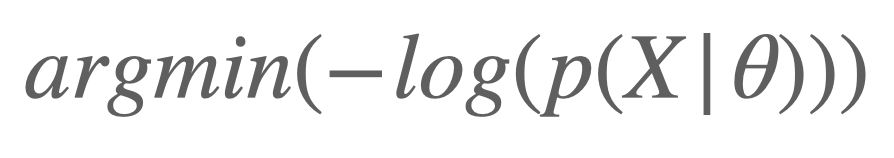
argmin의 요소로 바꾸기 위해 -값을 붙였으며, 확률의 곱으로 이루어진 Likelihood에 연산의 효율성을 위해 log를 씌우게 됩니다. 이를 Negative Log Likelihood라 부릅니다. 이제 확률 관점으로 머신러닝을 바라보기 위한 최소한의 개념을 배웠습니다. 만약 Likelihood와 MLE에 대해서 잘 이해가가지 않는다면 꼭 이해하고 넘어가시길 바라며, 아래에 유용한 자료를 첨부해 드립니다.
확률 관점으로 바라보는 머신러닝
확률 관점으로 머신러닝을 이해한다는 것은 다시 말해, 딥러닝 모델을 학습시키는 것과 Maximum Likelihood Estimation(MSE)과 같은 말이다 라는 걸 이해한다는 것입니다.

전체적인 해석을 완전히 달리 하는게 아닙니다. 단지 모델의 출력값과 Loss부분을 사뭇 다르게 해석해 보고자 합니다. 위의 그림에서 단계별로 살펴보자면,
- 학습데이터 x를 모델에 입력한다.
- 입력값 x가 모델 내의 파라미터(Weight and Bias)를 거쳐가며 특정 확률 분포의 파라미터인 $\theta$를 도출해 낸다. (해당 특정 확률 분포는 사전에 정의를 해줍니다. 보통 가우시안 분포 or 베르누이 분포를 사용하며, 가우시안 분포로 정의할 경우 $\theta$는 해당 분포의 파라미터인 평균과 표준편차가 됩니다.)
- 이렇게 얻은 값 $\theta$를 통해 사전에 정의한 확률 분포를 나타내고 Likelihood $p(Y_{true}|\theta)$ 를 구하게 된다.(이때의 $\theta$는 모델을 구성하는 파라미터가 아닌, 모델의 출력값인 확률 분포의 파라미터라는 걸 주의해야 합니다.)
- 이제 이 Likelihood가 최대가 되도록 하는 $\theta$를 찾기 위해 모델의 파라미터를 새롭게 갱신한다. (이 과정이 MLE라는 것을 위에서 배웠습니다.)
- 위의 과정을 계속 반복하며, Likelihood값이 최대가 되도록 학습을 진행한다. 즉, Likelihood가 가장 높은 $p(Y_{true}|\theta)$를 얻기 위해 $\theta$를 계속해서 수정해 나간다.
기존에는 모델의 출력값이 곧 예측값(y_pred)이었고, 이 값이 실제값(y_pred)이길 바라며 학습이 이루어졌습니다. 하지만 확률 관점으로 봤을 때는, 모델의 출력값은 특정 확률 분포를 결정짓는 파라미터($\theta$)이며, 이렇게 결정된 확률 분포가 Y_true에 대해 Likelihood값이 높아지길 바라며(MLE) 학습이 이루어집니다. 즉, 모델의 출력값은 y_pred가 아니라 Y_true를 잘 표현하고자 하는 확률 분포의 파라미터가 되는 것이고, Loss는 MSE나 Cross-Entropy가 아닌, Negative Log Likelihood(-log($p(Y_{true}|\theta)$))라는 것입니다.
그런데 여기서 재미있는 사실이 하나 있습니다. 우리가 관심 있는 확률 분포 $p(Y_{true}|\theta)$는 어떤 분포를 따를 것인지 사전에 미리 정의를 해준다고 했습니다. 이를 가우시안 분포로 할 건지, 베르누이 분포로 할건지 말이죠. 만약 해당 확률 분포가 가우시안 분포를 따른다고 가정해 본다면, -log($p(Y_{true}|\theta)$)는 MSE와 동일한 수식을 가지게 됩니다. 그리고 베르누이 분포를 따른다고 가정해 본다면, -log($p(Y_{true}|\theta)$)는 Cross-Entropy와 동일한 수식을 가지게 되죠. 즉, 기존의 머신러닝 관점에서의 Loss(MSE, Cross-Entropy)와 확률 관점으로 보는 머신러닝에서의 Negative Log Likelihood는 사실 동일한 수식을 가진다는 것이죠. 해석만 달리할 뿐. 그래서 우리는 아래와 같이 최종적으로 결론지을 수 있습니다.
딥러닝 모델을 학습시킨 다는 것은 Maximum Likelihood Estimation 하는 것과 같은 말이다.
굳이 어렵게 확률론적으로 해석할 필요가 있나?
기존에는 고정 입력(x)에 대한 고정 출력(y_pred)을 얻게 되었습니다. 하지만 확률 관점으로 보게 된다면, 우리는 고정 출력(y_pred)이 아닌, 확률 분포를 얻게 됩니다. Discrete 한 데이터를 통해 Continuous 한 확률 분포를 얻었으므로, 이제는 해당 분포로 부터 새로운 데이터를 샘플링하는 게 가능해졌습니다. 즉, 학습데이터를 잘 설명하는 분포를 얻었으니, 마치 학습데이터에 있을 법한 새로운 데이터를 뽑아낼 수 있게 됐죠. 그리고 이것이 생성모델의 핵심이라 볼 수 있습니다. 앞으로 나올 Variational AutoEncoder, GAN, Diffusion 등 여러 대표적인 생성모델을 이해하는 데에 있어서 확률 관점으로 머신러닝을 바라볼 수 있다면, 정말 큰 자산이 될 것입니다.
마치며..
역시 글로 풀어 설명하는 것은 정말 어려운 것 같습니다. 혹시나 이 글을 읽고 이해하려는 사람도 얼마나 힘들지 공감이 잘 됩니다. 설명하는 입장에서 최소한의 책임으로, 제가 해당 내용을 이해하는데 정말 도움 되었던 여러 reference를 추천하고자 합니다. 같은 내용에 대해서 여러 사람이 서로 다른 관점으로 설명하는 자료가 이해하는데 도움 많이 되었습니다. 그리고 해당 내용 중에 제가 잘못 이해하고 있는 부분이 있다면, 피드백 주신면 정말 감사하겠습니다!
Reference
- 머신러닝과 확률
https://www.notion.so/f3e308d9ab1f4224b3cc9726c1bd350c#5e5d047ca16f4d7facf0dfffb6f370ac - 오토인코더의 모든 것
https://youtu.be/o_peo6U7IRM - Maximum Likelihood란?
https://process-mining.tistory.com/93 - Baysesian Neural Network 내용 정리
https://gaussian37.github.io/dl-concept-bayesian_neural_network/
'Tech > Generative AI' 카테고리의 다른 글
| Rag : 나만의 LLM을 만들자 (0) | 2024.03.03 |
|---|---|
| GPTs, 나의 과거 프로젝트를 구현하다. (0) | 2024.01.21 |
| [StableDiffusion] Virtual Try On : 원하는 옷을 입혀보자 (1) | 2024.01.07 |
| [Stable Diffusion] ControlNet이란? ControlNet의 종류 (1) | 2023.09.16 |
| AutoEncoder (0) | 2023.03.19 |



